This post will cover some learnings from the algorithms & data structures module (COM00141M) during my MSc studies with the University of York.
What is a binary search Tree?
A binary search tree (BST) is a rooted binary tree data structure. It consists of a root at the top of the tree with accompanying child nodes. The root and nodes have either zero, one or two child nodes that form left and right subtrees.
Binary search trees have to satisfy the binary search property, meaning values in the left subtree must always be less than the parent and values in the right subtree must always be greater than the parent.
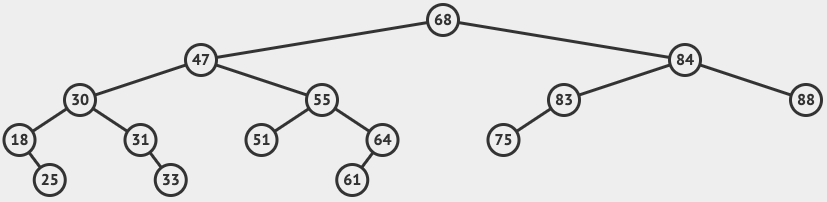
In the example above you can see a simple binary search tree conforming to the rules. If you read the tree from left to right you will note the order of the node values are ascending. The opposite descending form is apparent if you read from right to left.
What uses binary search trees?
Binary search trees allow for fast insertion, removal, searching and traversal of items. This makes them a good data structure to use to access or modify a collection whilst maintaining the order of elements. A few examples include priority queues, lookup tables and dynamic sets.
| Search | Insert | Delete | |
| Average (balanced) | 0(log n) | 0(log n) | 0(log n) |
| Worst (not balanced) | 0(n) | 0(n) | 0(n) |
What operations does a binary search tree have?
To demonstrate some of the algorithms in the next section, VisualGo will be used.
Searching
To find a value in a binary search tree you either use a recursive or iterative search algorithm. In most cases the iterative search is found to perform more efficiently and would resemble a while loop in implementation.
Recursive binary tree search
Recursive-Tree-Search(x, key)
if x = NIL or key = x.key then
return x
if key < x.key then
return Recursive-Tree-Search(x.left, key)
else
return Recursive-Tree-Search(x.right, key)
end if
Looking into the algorithm you can see it takes two values, x being the node in the tree to look at and a key equaling the value to search for.
The first if statement checks if the value is nil or equals the value being searched for, if true then x is returned and the recursion in this subtree ends as there are no further values to check. This is true because if nil is returned then there are no further child elements to look at so it must go back up a level and search another subtree or if it finds a match, the search is complete as we have found the target.
The second if statement checks if the value being searched for is less than the value being looked at, if true the search value is in the left subtree and if false it is in the right subtree, so it starts a recursive search in the correct subtree.
Let’s run through a simple example showing the recursive functionality:
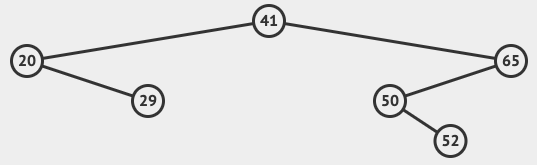
An example recursive binary search tree to find the value 52 from the above image.
- Recursive-Tree-Search(0, 52)
- x not nil and 41 != 52
- 52 < 41 = false
- RIGHT Recursive-Tree-Search(2, 52)
- x not nil and 65 != 52
- 52 < 65 = true
- LEFT Recursive-Tree-Search(4, 52)
- x not nil and 50 != 52
- 52 < 50 = false
- RIGHT Recursive-Tree-Search(5, 52)
- x not nil and 52 = 52
- return 5
- return 5
- return 5
- return 5
The value being searched for is at the node with an index of 5.
Iterative binary tree search
Iterative-Tree-Search(x, key)
while x ≠ NIL and key ≠ x.key then
if key < x.key then
x := x.left
else
x := x.right
end if
repeat
return x
The iterative approach achieves the same output but does so in one loop instead of creating recursive function calls.
Successor
The successor algorithm is used when you want to find the key value ascending relative to a node key in a binary search tree. This node equals the node with the next greater key than the key of the current.
BST-Successor(x)
if x.right ≠ NIL then
return BST-Minimum(x.right)
end if
y := x.parent
while y ≠ NIL and x = y.right then
x := y
y := y.parent
repeat
return y
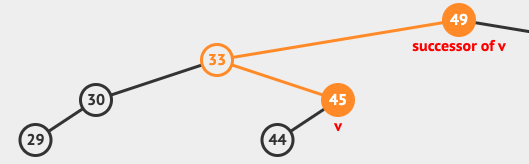
Here you can see that the successor of 45 would be 49.
If the node has a right subtree then it will use the BST-Minimum algorithm to find the the smallest value in the right subtree as that would be the successor.
The algorithm would have skipped the first if statement because 45 has no right subtree and instead it would have looped through the parent elements until it found the next right sided parent. If there was no right parent in the tree 45 would have been the highest element and no successor would be found.
Predecessor
BST-Predecessor(x)
if x.left ≠ NIL then
return BST-Maximum(x.left)
end if
y := x.parent
while y ≠ NIL and x = y.left then
x := y
y := y.parent
repeat
return y
The predecessor algorithm works in much the same way however it looks left instead of right.
If the node has a left subtree then it will use the BST-Maximum algorithm to find the the largest value in the left subtree as that would be the predecessor.
Insertion
To insert a value into a binary search tree we need to find the correct position for the value, this works in a similar style to searching for a value however instead of returning a found value it adds the new value to the tree.
1 BST-Insert(T, z) 2 y := NIL 3 x := T.root 4 while x ≠ NIL do 5 y := x 6 if z.key < x.key then 7 x := x.left 8 else 9 x := x.right 10 end if 11 repeat 12 z.parent := y 13 if y = NIL then 14 T.root := z 15 else if z.key < y.key then 16 y.left := z 17 else 18 y.right := z 19 end if
Deletion
To delete in a binary search tree we must be aware of how a deletion will affect child nodes, it is permitted to delete nodes that aren’t leaf nodes but we must then move the child nodes into the correct position.
1 BST-Delete(T, z) 2 if z.left = NIL then 3 Shift-Nodes(T, z, z.right) 4 else if z.right = NIL then 5 Shift-Nodes(T, z, z.left) 6 else 7 y := Tree-Successor(z) 8 if y.parent ≠ z then 9 Shift-Nodes(T, y, y.right) 10 y.right := z.right 11 y.right.parent := y 12 end if 13 Shift-Nodes(T, z, y) 14 y.left := z.left 15 y.left.parent := y 16 end if
There is a separate algorithm that is used to position the nodes in the correct order during a deletion.
1 Shift-Nodes(T, u, v) 2 if u.parent = NIL then 3 T.root := v 4 else if u = u.parent.left then 5 u.parent.left := v 5 else 6 u.parent.right := v 7 end if 8 if v ≠ NIL then 9 v.parent := u.parent 10 end if
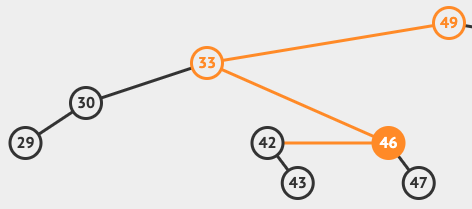
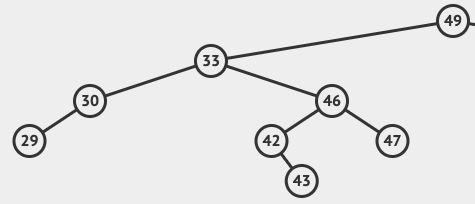
Traversal
The three traversal functions below allow us to access the data contained within the binary search tree in different formats.
Inorder tree walk
Travels through the tree from the left subtree nodes to the right subtree nodes, this produces an ascending order ouput.
Inorder-Tree-Walk(x)
if x ≠ NIL then
Inorder-Tree-Walk(x.left)
visit node
Inorder-Tree-Walk(x.right)
end if
Preorder tree walk
Travels in the same style as in order but returns the values as it visits them rather than in ascending order.
Preorder-Tree-Walk(x)
if x ≠ NIL then
visit node
Preorder-Tree-Walk(x.left)
Preorder-Tree-Walk(x.right)
end if
Postorder tree walk
Travels from the left subtree leaf node to the right subtrees finishing with the root.
Postorder-Tree-Walk(x)
if x ≠ NIL then
Postorder-Tree-Walk(x.left)
Postorder-Tree-Walk(x.right)
visit node
end if